“$500 + $500 Bounty Problem: An (Approximately) Deterministic Maximal Redund Always Exists” by johnswentworth, David Lorell

Audio note: this article contains 61 uses of latex notation, so the narration may be difficult to follow. There's a link to the original text in the episode description.

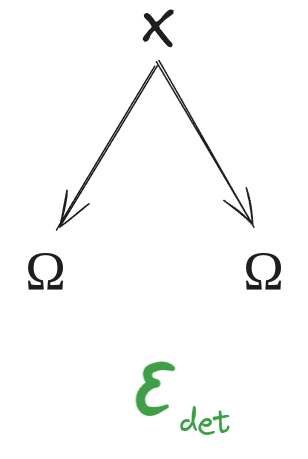
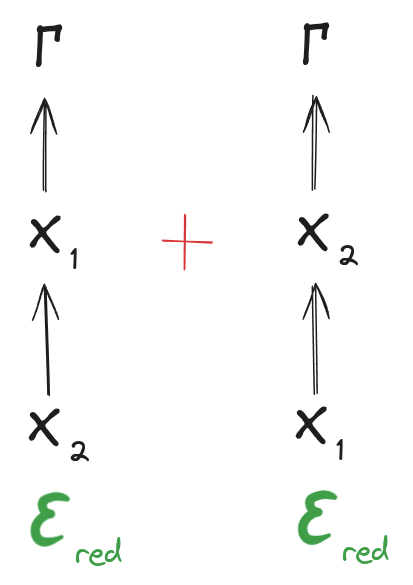
A lot of our work involves "redunds". A random variable <span>_Gamma_</span> is a(n exact) redund over two random variables <span>_X_1, X_2_</span> exactly when both

<span>_X_1 rightarrow X_2 rightarrow Gamma_</span>

<span>_X_2 rightarrow X_1 rightarrow Gamma_</span>

Conceptually, these two diagrams say that <span>_X_1_</span> gives exactly the same information about <span>_Gamma_</span> as all of <span>_X_</span>, and <span>_X_2_</span> gives exactly the same information about <span>_Gamma_</span> as all of <span>_X_</span>; whatever information <span>_X_</span> contains about <span>_Gamma_</span> is redundantly represented in <span>_X_1_</span> and <span>_X_2_</span>. Unpacking the diagrammatic notation and simplifying a little, the diagrams say <span>_P[Gamma|X_1] = P[Gamma|X_2] = P[Gamma|X]_</span> for all <span>_X_</span> such that <span>_P[X] > 0_</span>.

The exact redundancy conditions are too restrictive to be of much practical relevance, but we are [...]

---

Outline:

(02:31) What We Want For The Bounty

(04:29) Some Intuition From The Exact Case

(05:57) Why We Want This

---

First published:
May 6th, 2025

Source:
https://www.lesswrong.com/posts/sCNdkuio62Fi9qQZK/usd500-usd500-bounty-problem-an-approximately-deterministic

Narrated by TYPE III AUDIO.

---

Images from the article:

---

---

---

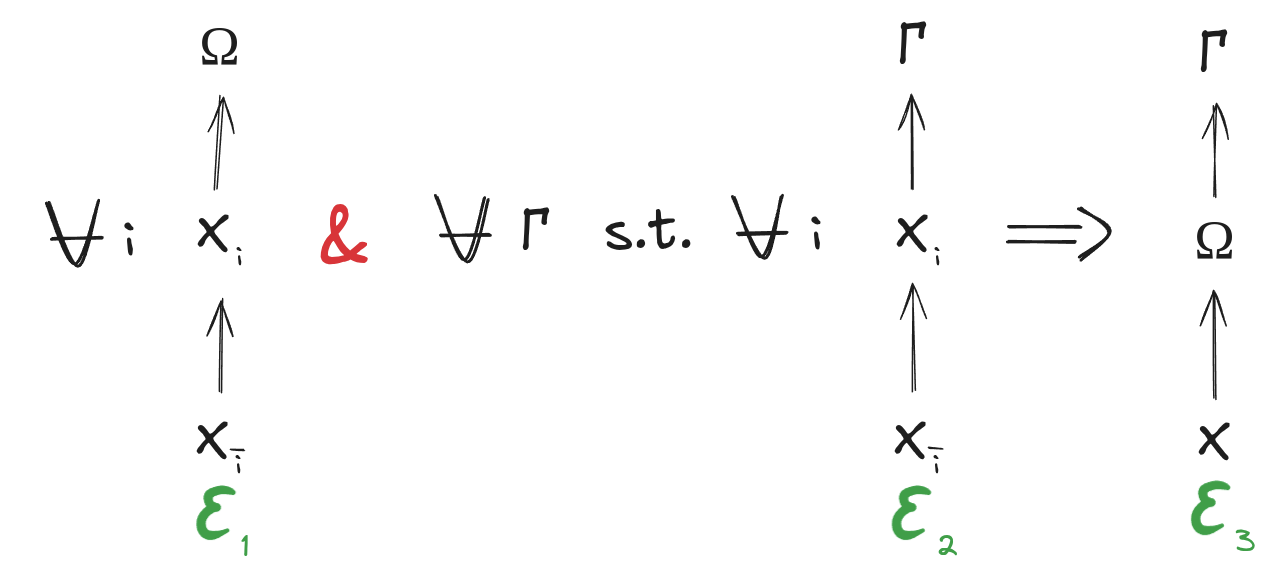
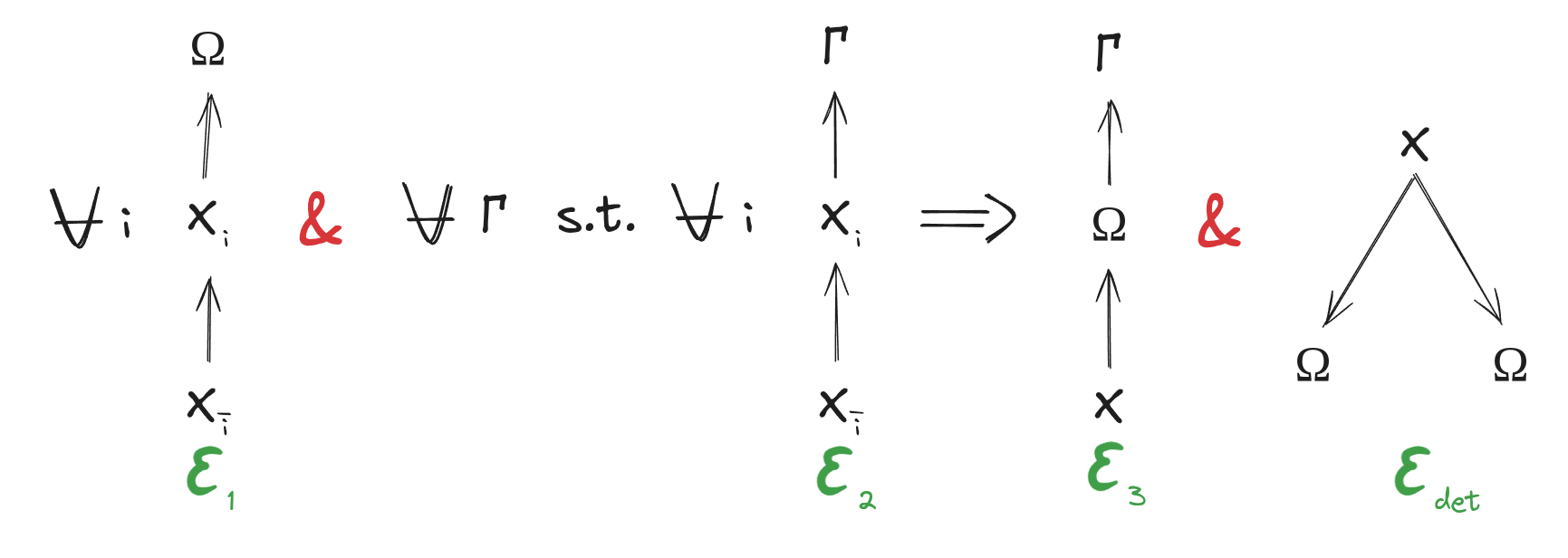
Apple Podcasts and Spotify do not show images in the episode description. Try Pocket Casts, or another podcast app.