LessWrong (Curated & Popular)
LessWrong (Curated & Popular) “A Straightforward Explanation of the Good Regulator Theorem” by Alfred Harwood
Jun 17, 2025
Explore the intriguing Good Regulator Theorem and its implications on system regulation. Discover why every good regulator must effectively model the system it governs. The discussion dives into key ideas like Bayes nets and Shannon entropy. An insightful critique of the theorem's original complexity is presented. Simplicity in regulator design is championed, emphasizing deterministic outputs to minimize entropy. Perfect for anyone keen on agent foundations and the nuances of selection theory.
AI Snips
Chapters
Transcript
Episode notes
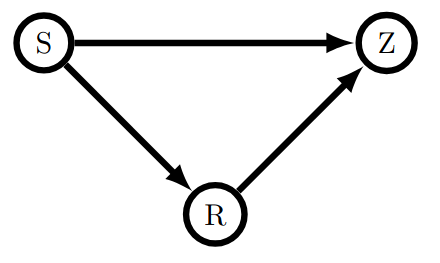
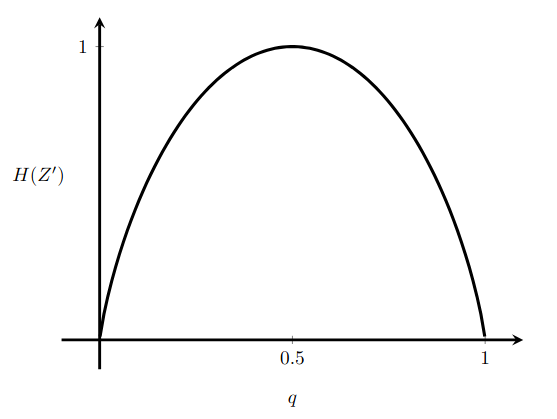
Low Entropy as Good Regulator Criterion
- Minimizing the Shannon entropy of the outcome variable is a measure of a good regulator.
- However, low entropy alone is not sufficient to ensure the regulator is useful or effective.
Unnecessary Complexity Reduces Quality
- A regulator that achieves minimum entropy without unnecessary randomness is considered better.
- Randomizing outputs unnecessarily increases complexity, making the regulator less good despite similar entropy outcomes.
Regulator as Deterministic Function
- The theorem states that a good regulator's output state is a deterministic function of the system state.
- This ties to the concavity of entropy, where increasing outcome imbalance lowers entropy, favoring deterministic mappings.